私は今、Aidemy Premium Planという、未経験者が3か月で機械学習、ディープラーニング、データ分析、AIアプリ開発まで最先端技術を幅広く学べるオンライン学習サービスで勉強しています。
データ分析コースで、時系列データ(時間の経過とともに変化するデータ)を予測する時系列分析について学びました。学んでみると、予測してみたい欲が湧いてきたので、時系列データの予測を実際にやってみました。
最初なので、季節性がわかりやすく存在し、感覚的にも予測できそうなデータを探したところ、コンビニエンスストアの月間売上のデータの予測をすることにしました。今回は、その予測の手順を紹介します。

Google Colaboratoryを使用しました。
データ取得
データ元
コンビニの月間売上のデータは、経済産業省の時系列データ『コンビニエンスストア商品別販売額』から取得します。excelでこんな感じで整理して、csvファイルでダウンロード(ファイル→ダウンロードから選択可能)します。
salesに関しては、コンマが入っていると文字列で出力されてしまうので、value()関数を使って数字に直しておくとよいです。1998-1 ~ 2019-10までの月間売上額データを取得しました。
グラフで表示
では、matplotlibでグラフで表示してみましょう。横軸が年月、縦軸が売上(百万円)。

同じような形(夏が売上が高く、冬の売上が低い)が1年ごとに並んでいるように見えます。つまり、1年間の周期性(季節性)を持っていそうです。また、右肩上がりのトレンドがあるのがわかります。
コードは以下。
# 時系列データを取得
import pandas as pd
from pandas import datetime
import numpy as np
import matplotlib.pyplot as plt
import csv
# csvファイルの読み込み
df = pd.read_csv('cvs_sales.csv',
index_col='moth', # インデックス列を指定
parse_dates=True) # 日付型に設定
# このままでと1998-01-01のように月始めになるので、インデックスを月末に変更
df.index=pd.date_range("1998-01-31", "2019-10-31", freq="M")
# グラフ表示
fig = plt.figure()
plt.xlabel("month")
plt.ylabel("sales")
plt.plot(df)
plt.show()
csvファイルの読み取りは、こちらのサイト(Pythonで時系列分析の練習(3)PandasでCSVファイルの読み込み)を参考にしました。
周期性(季節性)の確認
最終的にモデルに当てはめを行う際に、データに周期性(季節性)があるのか?によって使うモデルが異なります。また、周期性があるならその周期はいくらか?を知っておく必要があります。
今回は原系列のグラフから12か月の周期性(季節性)があることがわかりますが、通常は、自己相関係数や偏自己相関係数を可視化して調べるのが一般的です。
自己相関係数(ACF:Autocorrelation Function)
自己相関係数とは、過去の値とどれほど似ているのか(相関があるのか)を表す指標です。以下のように可視化したものはコレログラフと呼ばれます。
横軸はラグ(lag)です。例えば、ラグが1のときは、1つ前のデータがどのくらい影響を与えているかを表しています。ラグ0の場合は、同じ値同士の相関なので常に1になります。
ここで、色が濃くなっているところが95%信頼区間です。信頼区間の領域を超えてプロットされているデータは、統計的に有意差がある値といえます。
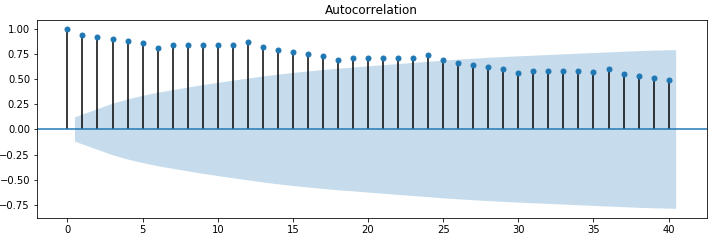
このグラフを見ると、ラグが6までは自己相関係数が少しずつ下がっていて、7で少しだけ上がり11までは横ばいで、12で少し高い値となっています。そして、この傾向が13以降も繰り返されているのがわかります。
12, 24, 36で少し高い値となっているということは、これは12か月の周期性(季節性)があるということを表しています。
偏自己相関係数(PACF, partial autocorrelation function)
偏自己相関係数は、自己相関係数と同じように過去の値とどれほど似ているのか(相関があるのか)を表す指標です。しかし、自己相関係数とはちょっと違います。
例えば、ある日のデータと、3日前のデータとの間で自己相関係数を求めると、2日前と1日前のデータの影響も含まれます。
一方、偏自己相関係数の場合は、2日前と1日前のデータの影響を取り除き、ある日のデータと3日前のデータをピンポイントで相関を求めることができます。間の影響を受けないピンポイント自己相関係数みたいな感じです。
可視化結果は以下。
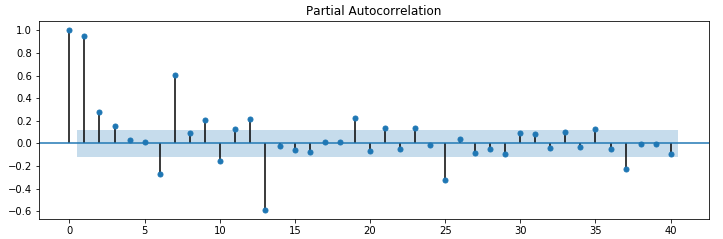
95%信頼区間領域を超えているラグ=1, 6,7,12,13, 25, 36のデータと相関が高い結果となっています。
一般的には、周期性(季節性)が12の場合は12で高い値となるはずです。ラグ = 12よりも、13で高い値となっているのはよくわかりません。
自己相関係数と偏自己相関係数の可視化の仕方は以下コード。
# 自己相関係数と偏自己相関係数の可視化
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
# csvファイルから読み込み
df = pd.read_csv("cvs_sales.csv",index_col=0)
# 自己相関・偏自己相関の可視化
fig=plt.figure(figsize=(12, 8))
# 自己相関係数のグラフを出力します
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df, lags=40, ax=ax1)
# 偏自己相関係数のグラフを出力します
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df, lags=40, ax=ax2)
plt.show()
階差系列
ひとつ前の値との差(差分)をとった後の系列を階差系列といいます。階差系列をとることでトレンドを取り除くことができます。df_diff = df.diff()。コードは以下。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
# csvファイルから読み込み
df = pd.read_csv('cvs_sales.csv',
index_col='moth',
parse_dates=True)
df.index=pd.date_range("1998-01-31", "2019-10-31", freq="M")
# データの階差をとる
df_diff = df.diff()
df_diff = df_diff.dropna() # NaNデータは捨てる
# グラフ表示
plt.subplot(2,1,1)
plt.title("original")
plt.xlabel("date")
plt.ylabel("sales")
plt.plot(df)
plt.subplot(2,1,2)
plt.title("Diff")
plt.xlabel("date")
plt.ylabel("sales diff")
plt.plot(df_diff)
plt.tight_layout() # グラフの間隔を自動調整
plt.show()
以下がオリジナル(上)と階差系列(下)のグラフです。トレンドがなくなっているのがわかります。
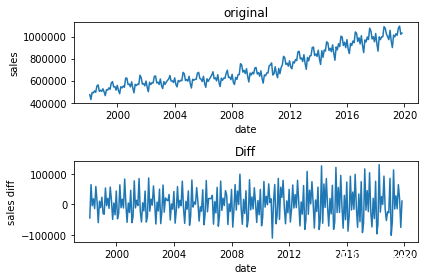
階差系列で自己相関係数と偏自己相関係数の可視化をすると、周期性(季節性)がわかりやすくなります。自己相関係数のグラフを見ると、12の周期性(季節性)がわかりやすく現れています。
偏自己相関係数に関しては、正直よくわかりません。

コードは以下。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
# csvファイルから読み込み
df = pd.read_csv("cvs_sales.csv",index_col=0)
# データの階差をとる
df_diff = df.diff()
df_diff = df_diff.dropna() # NaNデータは捨てる
# 自己相関・偏自己相関の可視化
fig=plt.figure(figsize=(12, 8))
# 自己相関係数のグラフを出力します
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_diff, lags=30, ax=ax1)
# 偏自己相関係数のグラフを出力します
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_diff, lags=30, ax=ax2)
plt.show()
トレンド、季節性、残差に分解
もうモデルの当てはめをして予測することができます。
ただその前に、時系列データをトレンド、季節性、残差に分解する方法を紹介しておきます。sm.tsa.seasonal_decompose を使うと、トレンド、季節性、残差に分解することができます。以下コードで分解してグラフ表示できます。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
# csvファイルから読み込み
df = pd.read_csv('cvs_sales.csv',
index_col='moth',
parse_dates=True)
df.index=pd.date_range("1998-01-31", "2019-10-31", freq="M")
# トレンド、季節性、残差に分解(周期は12)
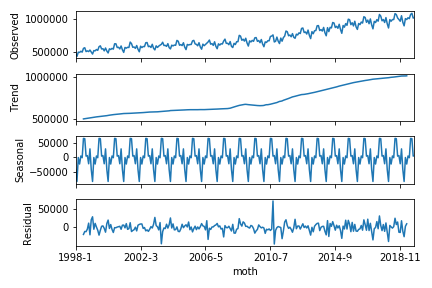
res = sm.tsa.seasonal_decompose(df, freq=12).plot()
plt.show()
こちらがグラフ。明らかに右肩上がりのトレンドがあるのがわかります。
SARIMAモデルで予測
トレンドがあり、季節周期があるのでSARIMAモデルで予測しましょう。
パラメータの選定
SARIMAモデルとはARIMAモデルをさらに季節周期を持つ時系列データにも拡張できるようにしたモデルです。このモデルは(p, d, q)のパラメーターのほかに(sp, sd, sq, s)というパラメーターを持ちます。
この中でsは周期を表します。今回は、12か月の季節性があるので s = 12です。
他のパラメータに関しては、BIC(ベイズ情報量基準)を元に、最適なパラメータを選びます。BICの値が小さいほど良いパラメータという理解です。
以下コードで、パラメータを取りうる範囲内で総当たりでモデルを作成して、BICを計算します。そして、一番BICが小さいパラメータの組み合わせを求めます。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from pandas import datetime
import numpy as np
import csv
# csvファイルを読み込む
df = pd.read_csv('cvs_sales.csv',
index_col='moth',
parse_dates=['moth'])
df.index=pd.date_range("1998-01-31", "2019-10-31", freq="M")
# 自動SARIMA選択
s = 12
max_p = 3
max_q = 3
max_d = 1
max_sp = 2
max_sq = 2
max_sd = 2
pattern = max_p*(max_q + 1)*(max_d + 1)*(max_sp + 1)*(max_sq + 1)*(max_sd + 1)
modelSelection = pd.DataFrame(index=range(pattern), columns=["order","season","bic"])
num = 0
for p in range(1, max_p + 1):
for d in range(0, max_d + 1):
for q in range(0, max_q + 1):
for sp in range(0, max_sp + 1):
for sd in range(0, max_sd + 1):
for sq in range(0, max_sq + 1):
sarima = sm.tsa.SARIMAX(
df, order=(p,d,q),
seasonal_order=(sp,sd,sq,s),
enforce_stationarity = False,
enforce_invertibility = False
).fit()
modelSelection.ix[num]["order"] = (p, d, q)
modelSelection.ix[num]["season"] = (sp, sd, sq)
modelSelection.ix[num]["bic"] = sarima.bic
num = num + 1
print(modelSelection)
# BIC最小モデル
print(modelSelection[modelSelection.bic == min(modelSelection.bic)])
結果は、(p, d, q) = (1, 1, 3)、(sp, sd, sq) = (0, 2, 2) で、BIC = 4770.78 4794.18 となります。これで、パラメータを決定できました。
モデルを当てはめて予測
1998年から2016年までのデータを学習用のトレインデータとします。
そして、2017年から2019年10月までの34点をテストデータとします。この34点は予測用です。本来は、未来のデータを予測しますが、本当に未来のデータを予測すると予測が正しいかどうかがわかりません。なので、ここでは、この34点を正解がある未来のデータとして予測します。
トレインデータに対して、モデルの当てはめをします。predがトレインデータの学習結果です。そして、pred2が学習を元に上記の34点を予測したデータです。
コードは以下。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from pandas import datetime
import numpy as np
import csv
# csvファイルの読み込み
df = pd.read_csv('cvs_sales.csv',
index_col='moth', # インデックス列を指定
parse_dates=True) # 日付型に設定
df.index=pd.date_range("1998-01-31", "2019-10-31", freq="M") # このままでと1998-01-01のように月始めになるので、月末に変更
# トレインデータとテストデータに分ける
N = len(df)
pred_point = 34
# 最新34点を予測する
df_train = df[:(N - pred_point)]
df_test = df[(N - pred_point):]
# トレインデータのモデルの当てはめ
SARIMA_df = sm.tsa.statespace.SARIMAX(df_train,order=(1, 1, 3),seasonal_order=(0, 2, 2, 12)).fit()
# predに予測データを代入する
pred = SARIMA_df.predict("1998-01-31", "2016-12-31")
pred2 = SARIMA_df.predict("2016-12-31", "2019-10-31")
# グラフ化
fig = plt.figure()
plt.plot(df_train, color="b")
plt.plot(df_test, color="b")
plt.plot(pred, color="r")
plt.plot(pred2, color ="y")
plt.show()
predがトレインデータの学習結果を赤、34点の予測結果を黄、そして、実データを青でグラフを描きます。最初の2年分くらいは、学習結果(赤)が実データ(青)と全くフィットしていませんが、その後は良いフィッティングとなっています。

予測部分(2017年から2019年10月までの34点)を拡大して見てみましょう。
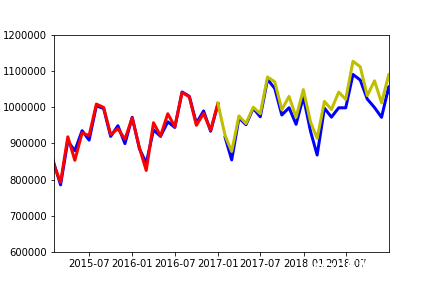
少しずれていますが、まずますの精度で予測ができているのがわかります。
予測データの評価
残差の自己相関・偏自己相関
SARIMAモデルの残差の自己相関・偏自己相関のグラフ化してみて、自己相関が全体的に小さいと良いモデルと言えます。
しかし、残差に自己相関が大きい部分があったり、周期性があるとダメなモデルと言えます。これは、残差は本来、トレンドや季節性を取り除かれているものなのに、周期性や自己相関が大きい部分があるのは、SARIMAモデルが周期性やトレンドをしっかり捉えたモデルになっていないと言えます。
SARIMAモデルSARIMA_dfの残差を求めて、自己相関・偏自己相関をグラフ化してみます。コードは以下。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from pandas import datetime
import numpy as np
import csv
# csvファイルの読み込み
df = pd.read_csv('cvs_sales.csv',
index_col='moth', # インデックス列を指定
parse_dates=True) # 日付型に設定
df.index=pd.date_range("1998-01-31", "2019-10-31", freq="M") # このままでと1998-01-01のように月始めになるので、月末に変更
# トレインデータとテストデータに分ける
N = len(df)
pred_point = 34
# 最新34点を予測する
df_train = df[:(N - pred_point)]
df_test = df[(N - pred_point):]
# モデルの当てはめ
SARIMA_df = sm.tsa.statespace.SARIMAX(df_train,order=(1, 1, 3),seasonal_order=(0, 2, 2, 12)).fit()
sarimax_resid = SARIMA_df.resid
# sarimax_resid = sarimax_resid[36:]
# モデル残差のコレログラム
fig = plt.figure(figsize=(8, 8))
# 自己相関(ACF)のグラフ
ax1 = fig.add_subplot(211)
sm.graphics.tsa.plot_acf(sarimax_resid, lags=40, ax=ax1) #ACF計算とグラフ自動作成
# 偏自己相関(PACF)のグラフ
ax2 = fig.add_subplot(212)
sm.graphics.tsa.plot_pacf(sarimax_resid, lags=40, ax=ax2) #PACF計算とグラフ自動作成
plt.tight_layout() # グラフ間スキマ調整
自己相関・偏自己相関のグラフは以下。

がっつり、12か月の周期性残っています。また、ラグ1も大きな値となっていて自己相関が残っています。つまり、あまり良いモデルとは言えません。。。
最初の2年くらいの学習結果が実データと全くフィッティングしていない部分が悪影響なのかと思い、最初の36点を残差計算から外してみます(sarimax_resid = sarimax_resid[36:])。

ラグ1が小さい値となりましたが、12か月の周期性はまだ残っています。改善の余地はまだまだありそうですが、今回は、予測がそこそこうまくいっているのでここで終わりとします。
終わりに
今回、初めて時系列データ分析を行い、SARIMAモデルで『コンビニ売上』の予測を行いました。実際に予測を行ってみると理解が深まりました。が、まだまだよくわからず、今回の予測も改善すべきところは多いと思います。

以下、参考にしたサイトです。めちゃめちゃわかりやすいサイトでした。感謝です。
参考サイト1:Python時系列分析(ALL) in もものきとデータ解析をはじめよう参考サイト2:SARIMAで時系列データの分析(PV数の予測)



[…] コンビニの売上予測分析 […]
[…] https://toge510.com/2019/12/26/predictionsalesofcvsbysarimamodel/#ACFAutocorrelation_Function […]
[…] https://toge510.com/2019/12/26/predictionsalesofcvsbysarimamodel/#ACFAutocorrelation_Function […]